Recognition of Hand Written Mathematical Expression using Scale Augmentation and Drop Attention

Abstract

This is a review paper. We start by explaining about how handwritten mathematical expressions have unstable scale.Then we show how augmented layers are used for scaling those mathematical expression.We continue by explaining how an attention based encoder-decoder is used for extracting features and generating predictions.The drop attention is used when the attention distribution of the decoder is not precise.This method achieves better performance than any other existing method.

1. Introduction

In this section we will discuss the problem we are addressing and how we are going to tackle the problem. So we are trying to convert Hand Written Mathematical Expressions to .tex format. One of the main problem that arises when converting Hand Written Mathematical Expression is scaling the image of the Mathematical Expression.

The main thing in this process of converting the Hand Written Mathematical Expression to .tex is the encoder-decoder network.We enhance this network by using Scale Augmentation at the beginning and Drop Attention at the end to enchance the accuracy which increases quality of this output.

Sketch of the Paper

•Encoder-Decoder Network
•Scale Augmentation
•Drop Attention
•Experiment and Implementation
•Conclusion
•References

Sketch of the process

•Scale Augmentation
•Encoder-Decoder network
•Drop Attention

As we can see the Scale Augmentation is used at the begining before the Encoder-Decoder Network but it is used to enhance the Encoder-Decoder Network. So we need to understand what is the Encoder-Decoder Network then we can move on with Scale Augmentation.

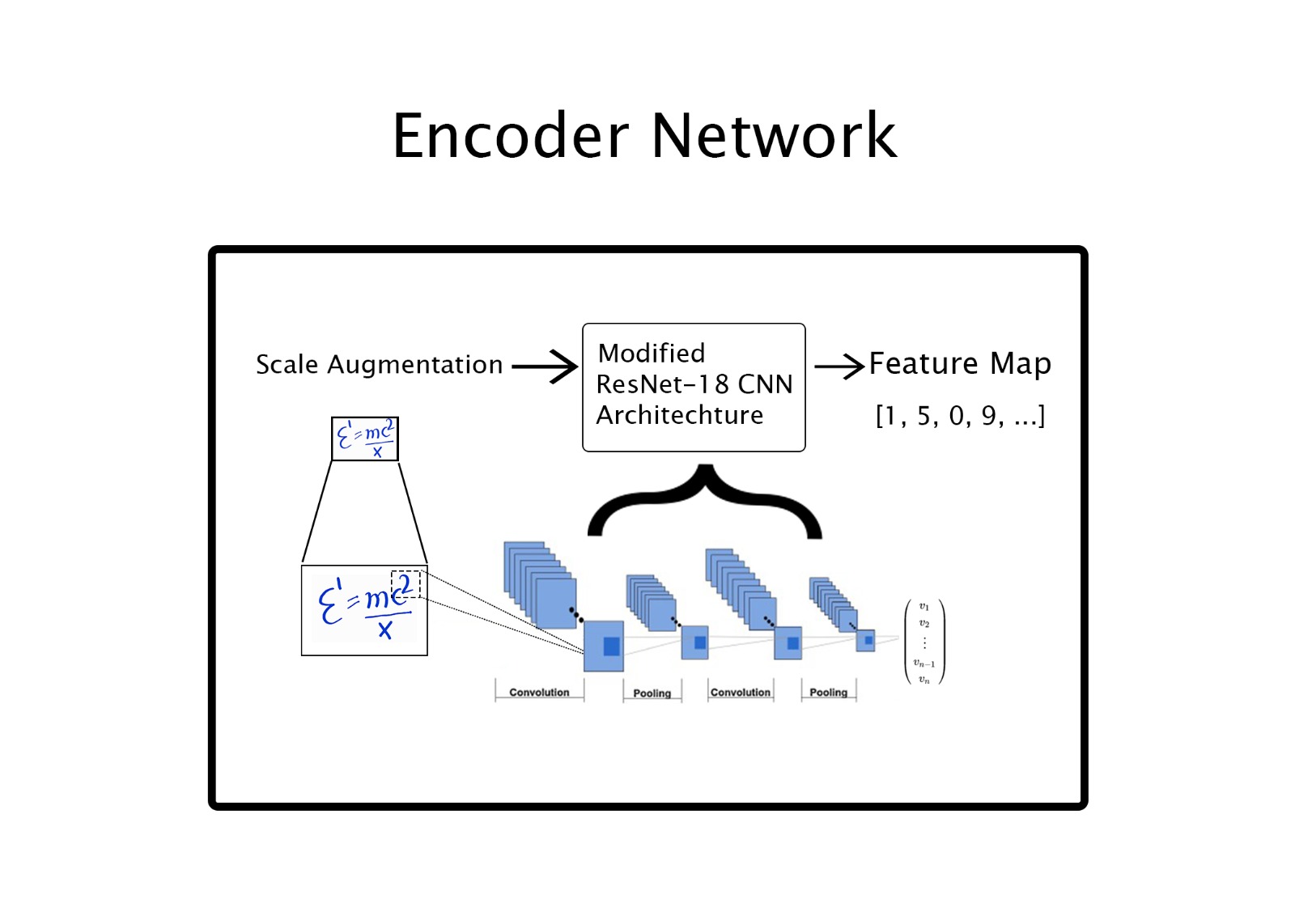
2. Encoder-Decoder Network

The encoder is build by modifying the CNN architechture ResNet-18 and we set the stride of all convolutional layers in ResNet-18 to 1 in order to extract the more precise features and avoid the neglecting features.The other settings are same as in [1] .Max pooling layers are used for down-sampling and dropout layers are used to lessen the network over fitting.The detailed network configuration is shown in the table I.

Variables and their Meanings

•c - Number of filters
•k - Kernel number
•s - Kernel Size
•pa - Stride Padding
•n - Block Number
•p - Dropout Probability

Table I(detailed Network Configuration)

\begin{array}{cc} Layer/Block & Setting \\ Convolution & c = 64, k = 3 \times 3, s = 1, p a = 1 \\ Max pooling & k = 2 \times 2, s = 2 \\ Batch norm & - \\ ReLU & - \\ Building block & c = 64, n = 2 \\ Max pooling & k = 2 \times 2, s = 2 \\ Dropout & p = 0.1 \\ Building block & c = 128, n = 2 \\ Max pooling & k = 2 \times 2, s = 2 \\ Dropout & p = 0.2 \\ Building block & c = 256, n = 2 \\ Max pooling & k = 2 \times 2, s = 2 \\ Dropout & p = 0.3 \\ Building block & c = 512, n = 2 \\ Max pooling & k = 2 \times 2, s = 2 \\ Dropout & p = 0.3 \end{array}

The attention-based decoder is based on RNN and iteratively generates the target sequence Y from features F.

Definition(Softmax Function) :The softmax function is a function that turns a vector of K real values into a vector of K real values that sum to 1. The input values can be positive, negative, zero, or greater than one, but the softmax transforms them into values between 0 and 1, so that they can be interpreted as probabilities.

σ (\vec{z})_{i} = \frac{e^{z_{i}}}{\sum_{j = 1}^{K} e^{z_{j}}}

• $σ = softmax$
• $\vec{z} =$ input vector
• $e^{z_{i}} =$ standard exponential function for input vector
• $K =$ number of classes in the multi-class classifier
• $e^{z_{j}} =$ standard exponential function for output vector
• $e^{z_{j}} =$ standard exponential function for output vector

Variables and their Meanings

•t - time step
• $y_{t}$ - A member of the target sequence Y at time step t
• $c_{t}$ - context at time step t
• $h_{t}$ - hidden state at time step t
• $H$ - Height of the feature F
• $W$ - Width of the feature F
• $L$ - the size of the features $L = H \cdot W$
• $α_{t, l}$ - weight of the $l^{t h}$ features of F at time step t
• $f_{l}$ - the $l^{t h}$ features of F
• $\tanh$ - chosen activation function
• $e_{t, l}$ - attention weight of the $l^{t h}$ features of F at time step t
• $W^{e}, W^{h}, W^{f}, W^{q}, W^{s}$ - trainable Parameters
• $q_{l}$ - position embedding of the $l^{t h}$ features of F
• $s_{l}$ - coverage features of the $l^{t h}$ features of F
• $E^{p, h}$ - absolute position embedding in horizontal direction
• $E^{p, v}$ - absolute position embedding in vertical direction

At t the probability of generating

y_{t}

from the RNN output is shown in the equation 1 where

g (\cdot)

is a linear function followed by a softmax function.

\begin{matrix} (1) & p (y_{t}) = g (c_{t}, h_{t}) \end{matrix}

Context

c_{t}

is computed as a weighted sum of features in equation 2.

\begin{matrix} (2) & c_{t} = \sum_{l = 0}^{L - 1} α_{t, l} \cdot f_{l} \end{matrix}

Similar to human eyes the attention based decoder concentrates on only a subset of features at a time.Trained using back propagation algorithm using gradient descent,the decoder can be given the ability to determine which features are important for generating the word

y_{t}

.We choose a linear function with the activation function

\tanh

.We compute the attention weights and normalization using softmax function as shown in equation 3 and equation 4 respectively.

\begin{matrix} (3) & e_{t, l} = W^{e} \tanh (W^{h} h_{t} + W^{f} f_{l} + W^{q} q_{l} + W^{s} s_{l}) \end{matrix}

\begin{matrix} (4) & α_{t, l} = \frac{\exp (e_{t, l})}{\sum_{i = 1}^{L} \exp (e_{t, i})} \end{matrix}

Refer to [2] when calculating the attention weights, position embeddings make the decoder position sensetive.The calculation of position embedding is shown in equation 5.

\begin{matrix} (5) & q_{l} = E^{p, h} (⌊ l / H ⌋) + E^{p, v} (l mod H) \end{matrix}

Referring to [3] the coverage features are used to lessen over-attention and under-attention.

s_{l}

is given as the sum of past attention weights in equation 6.

\begin{matrix} (6) & s_{l} = \sum_{τ = 0}^{t - 1} α_{τ, l} \end{matrix}

The hidden state is calculated using a RNN with long short- term memory (LSTM) cells. At time step t, the RNN input is the word embedding at t−1 concatenated with context at t−1, which is a weighted sum of CNN features F with position embeddings at last time step is represented by equation 8.

\begin{matrix} (7) & h_{t} = R N N ([E^{d} (y_{t - 1}), c_{t - 1}^{'}], h_{t - 1}) \end{matrix}

\begin{matrix} (8) & c_{t}^{'} = \sum_{l = 1}^{L} α_{t, l} \cdot (f_{l} + q_{l}) \end{matrix}

3. Scale Augmentation

Since in a Mathematical Expression the expression consists of various symbols some smaller than the others which increases the recognition difficulty. So we apply augmentation to the Mathematical Expression according to equation 9 to improve the recognition.

\begin{matrix} (9) & {\begin{cases} x^{'} = k x \\ y^{'} = k y \end{cases} \end{matrix}

k

is the scaling factor and we keep the aspect ratio unchanged.The encoder-decoder network is trained to adapt to Mathematical Expression of various scales in order to generate correct predictions.

4. Drop Attention

The normalised attention weight

α

has a great impact on recognition performance so when the attention neglects the key features, the model will generate an incorrect prediction which will result in worse performance.From [4] a different idea can be proposed that is the Drop Attention Module in the decoder.First, we randomly supress the features where the

α

is the highest.Then we randomly abandon spots according to equation 10.

Variables and their meanings

• $γ$ - Supress Factor
• $r_{p}, r_{s}$ - Random Variables that obey Bernoulli Distribution
• $f_{l}^{'}$ - features (replaces $f_{l}$ in equation 2 and 8 in training phase to predict the correct symbol when the attention is imprecise)

\begin{matrix} (10) & f_{l}^{'} = {\begin{array}{cc} γ \cdot f_{l}, & if l = argmax (α_{l}) and r_{p} = 0 \\ 0, & if l \neq argmax (α_{l}) and r_{s} = 0 \\ f_{l}, & otherwise \end{array} \end{matrix}

5. Experiment and Implementation

The proposed model was implemented using PyTorch and optimized on Nvidia TITAN

X_{p}

Graphical Processing Unit.For simultaneous calculations to be carried out at the same time the batch size was set to 8.The Mathematical Expression images underwent scale augmentation in the training phase and were zero padded to a fixed size

256 \times 1024

.Few of the mathematical expression were downsized because they were larger than the size before zero padding.The scaling factor(equation 9) k was set randomly within the bound

[0.5, 2]

during each training iteration.Using CNN the features were extracted and fed to the attention based decoder with configurations according to Table I.The suppress factor

γ

and the Bernoulli probabilities

r_{p}, r_{s}

(equation 10) during the training phase were set to

0.1, 0.8 and 0.4

respectively.The cross-entropy loss was calculated between the generated symbols and the ground truth.Adam optimizer was used to train the model, and the learning rate was

0.0001

5.1. Effect of Scale Augmentation

Comparative experiments for processing Mathematical Expression images were performed without applying the drop attention module.The three methods used are as follows :

•Normalization to a fixed height of 256 without changing the aspect ratios.
•Zero Padding to a fixed size.
•Scale Augmentation

The expression recognition rate for the above mentioned methods is shown in Table II.

(Expression Recognition Rate % of different processing methods for Mathematical Expression Images)

\begin{array}{ccc} Method & CROHME2014 & CROHME2016 \\ Normalized to fixed height & 48.78 & 49.26 \\ Zero - padded to fixed size & 50.00 & 47.95 \\ Scale Augmentation & 55.17 & 52.48 \end{array}

Table II[5]

It can be seen from Table II,the results with a fixed height normalization are slightly better than zero padding on the CHROME 2016 data set but worse on CHROME 2014.Whereas Scale Augmentation outperforms the other two methods which shows that Scale Augmentation is more effective than the other two methods.The model trained with Scale Augmentation could extract par subsection{Effect of Drop Attention} Comparative experiments were performed with and without the Drop Attention to verify its effectiveness.The results are shown in Table III.

(Expression Recognition Rate % of processing methods with or without Drop Attention)

\begin{array}{ccc} Drop Attention & CROHME 2014 & CROHME 2016 \\ without & 55.17 & 52.48 \\ with & 56.59 & 54.58 \end{array}

Table III[5]

As shown above in Table III when the experiment was performed with the Drop Attention Module, the accuracy improves by 1.42% on CROHME 2016 and 2.1% on CROHME 2014.The drop attention module trains model generating better predictions when attention neglects the key features.The Drop Attention model was implemented during the training phase of subsequent experiments to improve the performance of the proposed model.

5.2. Comparison with proposed methods

The graphs below shows the expression recognition rate(ExpRate) taken out using recent offline attention based Hand Written Mathematical Expression models on CROHME 2014 and CROHME 2016 datasets. Among all the Hand Written Mathematical Expression models, the Scale Augmentation and Drop Attention model (SADA[5]) achieves the best performing results.

6. Conclusion

In this paper Scale Augmentation method is used to solve the problem of recognition of Mathematical Expression of various scales. The problem is caused due to its two dimensional structure.A new Drop Attention module is used to enhance the training of the model which helps to generate better results when the attention is imprecise.The experimental results indicated that these two technologies assist our method achieving state-of-the-art performance, compared with the previous methods without an ensemble.

7. References

K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVRP), pp. 770–778, 2016
J.-W. Wu, F. Yin, Y.-M. Zhang, X.-Y. Zhang, and C.-L. Liu, “Handwrit- ten mathematical expression recognition via paired adversarial learning,” International Journal of Computer Vision, pp. 1–16, 2020.
J. Zhang, J. Du, S. Zhang, D. Liu, Y. Hu, J. Hu, S. Wei, and L. Dai, “Watch, attend and parse: An end-to-end neural network based approach to handwritten mathematical expression recognition,” Pattern Recognition, vol. 71, pp. 196–206, 2017.
G. Sun, H. Cholakkal, S. Khan, F. S. Khan, and L. Shao, “Fine-grained recognition: Accounting for subtle differences between similar classes,” arXiv preprint arXiv:1912.06842, 2019.
Z. Li, L. Jin, S. Lai and Y. Zhu, "Improving Attention-Based Handwritten Mathematical Expression Recognition with Scale Augmentation and Drop Attention," 2020 17th International Conference on Frontiers in Handwriting Recognition (ICFHR), Dortmund, Germany, 2020, pp. 175-180, doi: 10.1109/ICFHR2020.2020.00041.
H. Mouchere, C. Viard-Gaudin, R. Zanibbi, and U. Garain, “Icfhr 2014 competition on recognition of on-line handwritten mathematical expressions (crohme 2014),” in 2014 14th International Conference on Frontiers in Handwriting Recognition (ICFHR), pp. 791–796, IEEE, 2014.
A. D. Le and M. Nakagawa, “Training an end-to-end system for handwritten mathematical expression recognition by generated patterns,” in 2017 14th IAPR International Conference on Document Analysis and Recognition (ICDAR), vol. 1, pp. 1056–1061, IEEE, 2017.
J.-W. Wu, F. Yin, Y.-M. Zhang, X.-Y. Zhang, and C.-L. Liu, “Image- to-markup generation via paired adversarial learning,” in Joint Euro- pean Conference on Machine Learning and Knowledge Discovery in Databases, pp. 18–34, Springer, 2018.
A.D.Le,B.Indurkhya,andM.Nakagawa,“Patterngenerationstrategies for improving recognition of handwritten mathematical expressions,” Pattern Recognition Letters, vol. 128, pp. 255–262, 2019.
Z. Xie, Z. Sun, L. Jin, H. Ni, and T. Lyons, “Learning spatial-semantic context with fully convolutional recurrent network for online handwritten chinese text recognition,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 40, no. 8, pp. 1903–1917, 2017.
H. Mouche`re, C. Viard-Gaudin, R. Zanibbi, and U. Garain, “Icfhr2016 crohme: Competition on recognition of online handwritten mathematical expressions,” in 2016 15th International Conference on Frontiers in Handwriting Recognition (ICFHR), pp. 607–612, IEEE, 2016.
Y.Deng,A.Kanervisto,andA.M.Rush,“Whatyougetiswhatyousee: A visual markup decompiler,” arXiv preprint arXiv:1609.04938, vol. 10, pp. 32–37, 2016.
J. Zhang, J. Du, and L. Dai, “Multi-scale attention with dense encoder for handwritten mathematical expression recognition,” in 2018 24th International Conference on Pattern Recognition (ICPR), pp. 2245– 2250, IEEE, 2018.