Information Theory in Machine Learning
Introduction
Information can be represented as bits. One bit of information allows us to choose between two equally probable, or equiprobable, alternatives. In other words, in a scenario with 2 equiprobable choices, if you get an instruction to choose one of the choices, that is one bit of information. Say, each instruction can be represented as a binary digit (0='choice 1' and 1='choice 2') then this binary digit provides you with one bit of information. In the case of 'n' sequential forks, with 'm' final choices (destinations), then m= 2n. In other words, n= log2m. Information is thus, an ordered symbol of sequences to interpret its meaning.
Please note: A binary digit is the value of a binary variable, whereas a bit is an amount of information. A binary digit (when averaged over both of its possible states) can convey between zero and one bit of information.
By now, we know what information means. It is a mathematical representation of uncertainty. Let us now understand what information theory is.

Figure 1: A binary symmetric channel showing probability of incorrect transmission of message given the transmitted symbol is x and the received symbol is y
When we transmit data, for instance, a string of bits, over a communication channel or any computational medium, there is a probability (say 'p') that the received message will not be identical to the transmitted message. An ideal channel is where this probability (p) is zero (or almost 0). However, most real world channels have a non zero probability 'f' of incorrect transmission of information and a probability of (1 minus f) that each bit of information will be transmitted correctly. Given this probability of error, one needs to find solutions to reduce the same in order to transmit information with minimum error. One can use the 'physical solution' where one needs to revamp the physical attributes of the communication channel, for instance the circuitry. However, this might increase the operational cost. An alternative solution is to update the system using 'information theory' and 'coding theory'. Under these solutions, we accept the given noisy physical channel in its current form. We then add communication systems to it so that we can detect and correct the errors introduced by the channel. This system normally comprises of an encoder and decoder. The 'system' solutions can help you design a reliable communication channel with the only additional cost of computations of an encoder and a decoder. While coding theory helps you design the appropriate decoder and encoder, information theory helps you define the quality of information or content you can transmit. It can help you study the theoretical limitations and potentials of a system.
Information theory treats information as a physical entity, like energy or mass. It deals with theoretical analyses of how information can be transmitted over any channel: natural or man-made. Thus, it defines a few laws of information. Let us assume a basic system for information flow as follows:

Figure 2: Information Channel: A message (data) is encoded before being fed into a communication channel, which adds noise. The channel output has the encoded message with noise that is decoded by a receiver to recover the message.
There are a few laws on information that can be derived from the above channel:
- There is a definite upper limit, the channel capacity, to the amount of information that can be communicated through that channel.
- This limit shrinks as the amount of noise in the channel increases.
- This limit can very nearly be reached by judicious packaging, or encoding, of data.
Essentially, information theory entails two broad techniques:
- Data Compression (source coding): More frequent events should have shorter encodings
- Error Correction (channel coding): Should be able to infer encoded event even if message is corrupted by noise
Both these methods require you to build probabilistic models of the data sources. This is why information theory is relevant to machine learning and data analytics. It not only helps you measure the accuracy of information contained in a data source, but also helps you improve results of predictive models that might be built on this data. Before we study how information theory can be applied to, let us study a few basic terms.
Few important terms of Information Theory and Machine Learning
Codewords
Information theory represents data in the form of codewords. These codewords are representation of the actual data elements in the form of sequence of binary digits or bits. There are various techniques to map each symbol (data element) with the corresponding codeword.
Variable Length Codes
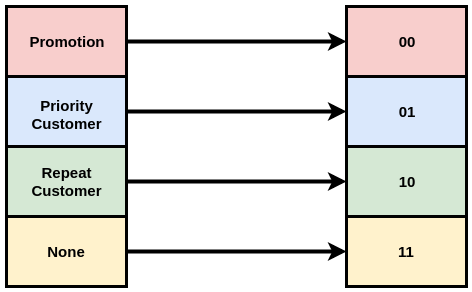
One traditional way of assigning codewords to data elements would be to assign codes with fixed lengths, or every data element gets assigned a code of the same code length. Let us look at a visual representation of the same. If we have 4 values of a given variable, say 'Discount type' with the following 4 values: 'Promotion', 'Priority Customer', 'Repeat buy' and 'None'. If we assume that the 4 types of discounts are equally probable, they can safely be mapped to codewords of equal length, say 00, 01, 10 and 11, as shown in the image below:

Figure 3: Fixed Length Encoding: Every data element here is assumed to have equal likelhood of occurrence. Hence, every code word have equal and fixed length (i.e. 2)
Now, if we know that discounts under 'Promotion' are more frequent than the rest and have been assigned the following probability values.

Figure 4: Varying probabilities of each data element indicating the likelihood of occurrence of the event
We can then, design codes weighted according to these probability values. We design the code to reduce the total length of the message. Since one would transmit the most frequent terms (data elements) most number of times, you would want to associate the least length with the most frequent term. Hence, we design a code with the least number of bits for the most frequent data element. Let us look at an example of the same.

Figure 5: Variable Length Encoding: Every data element has been mapped to a sequence of binary codes of varying length according to the probability of occurrence
This variable-length code will now represent each data element in a unique and exclusive manner. Moreover, if you consider the vertical axis to visualize the probability of each word, p(x), and the horizontal axis to visualize the length of the corresponding codeword, L(x), let us compute the area covered by the encoding. This amounts to 1.75 bits, which is a reduction from a fixed-length encoding of 2 bits each for all the above terms. The fixed-length encoding would amount to 2 bits.
Optimal Encoding
The most optimal encoding has to strike a balance between the length of the message and the cost of the codeword. Let us look at how one affects the other. The cost of buying a codeword of length 0 is 1. This is because you are buying all possible codewords, and hence, if you want to have a codeword of length 0, you can’t have any other codeword. The cost of a codeword of length 1, like "0" or "1", is (1/2) because half of possible codewords start with "0" or "1" respectively. The cost of a codeword of length 2, like “01”, is (1/4) because a quarter of all possible codewords start with “01”. In general, the cost of codewords decreases exponentially with the length of the codeword.
Refer to the image below:

Figure 6: Cost of a codeword as a function of the length of the codeword
We know that the average length of the total code string is the function of the probability of each word and the length of the corresponding codeword. It can be represented as

Figure 7: Relationship between Average Length Contribution and Cost of the Codeword
Thus, we can clearly establish that shorter codewords cost higher and vice versa.

Figure 8: Costs of long and short codewords
Shannon Information Content
Let us consider a set of discrete random variables 'X' which contains a possible set of events {
Thus, the information you can gain when an event occurs which had some probability value associated with it, can be represented as:
The above equation will show that as the value of probability 'p' increases, the information content decreases. You get a curve that looks something like this:

Figure 9: The information content function versus probability values
The information content is measured in bits. It is also known as self information.
Entropy
While designing an optimal codeword for our data elements above, we see that the average length contribution of a message and the cost of the same line up well. In other words, the height of the rectangle denoting the average length contribution of messages is almost equal to the maximum height of the exponential curve denting the cost of the codeword. Thus, if we slightly increase the length of the codeword, the message length contribution will increase in proportion to its height at the boundary, while the cost will decrease in proportion to its height at the boundary.

Figure 10: Proportionality of cost with the height of the message length contribution
We can also say that the cost to make the codeword for a data element 'a' shorter is p(a). Now, let us generalize this to any message 'X'. For a message 'X' with the likelihood of occurrence
As we discussed earlier, there is a limit to how short an average message can get to communicate events effectively, from a particular probability distribution 'p' of events 'X'. This limit, the average message length using the best possible code, is called the entropy or Shannon entropy of 'p',
Conditional Entropy
The average uncertainty about the output value (say 'Y') given an input value ('X') is the conditional entropy
The above equation can further be condensed into the following form:
You could modify this equation for a given value of the input, say
Cross Entropy or Joint Entropy
If X and Y are discrete random variables and p(X,Y) is the value of their joint probability distribution at (, y), then the joint entropy or cross entropy of X and Y is:
Let's say you have two discrete distributions: p(x) and q(x) with common elements. One way of defining cross entropy would be:
the average length of code for communicating an event from one distribution with the optimal code for another distribution is called the cross-entropy. It can be represented so:
For continuous distributions, you can simply replace the discrete summation with integral functions. Cross-entropy is an important measure. It gives us a way to show how different two probability distributions are. The more different the distributions 'p' and 'q' are, the more the cross-entropy of 'p' with respect to 'q' will be bigger than the entropy of 'p'.
Mutual Information
Let us consider a channel with inputs 'x', output 'y' and noise

Figure 11: Channel design demonstrating an ideal communication channel
In the above channel
In terms of 2 two random variables 'X' and 'Y' , whose joint distribution is defined by
Another metric that can be derived from the mutual information is the variation of information. The variation of information is the information which isn’t shared between these two variables ('x' and 'y'). We can define it like so:
The variation of information between two variables is zero if knowing the value of one tells you the value of the other and increases as they become more independent.
Conditional Mutual Information
The conditional mutual information is defined as the expected value of the mutual information of two random variables given the value of a third. For random variables X, Y, and Z, it can be represented as

Figure 12: Channel design demonstrating an ideal communication channel
Mathematically, it can be defined as:
This can be simplified to:
The above entity is greater than '0' for discrete, jointly distributed random variables X, Y and Z. The above probability mass functions represented by 'p' can be evaluated using conventional definitions of probability.
Multivariate mutual information
Multivariate mutual information (MMI) or Multi-information is the amount of information about Z which is yielded by knowing both X and Y together is the information that is mutual to Z and the X,Y pair, written as
Positive MMI is typical of common-cause structures. For example, clouds cause rain and also block the sun; therefore, the correlation between rain and darkness is partly accounted for by the presence of clouds,
Channel Capacity
The measure channel capacity basically helps us answer how fast can we transmit information over a communication channel. One of the most common and convenient channels used is the additive channel. This channel adds noise (
where
The rate at which information is transmitted through a channel can be determined using the entropies of three variables:
- the entropy
of the input, - the entropy
of the output, - the entropy
of the noise in the channel.
A output entropy is high then this provides a large potential for information transmission. It depends on the input entropy and the level of noise. If the noise is low, then the output entropy can be as close to the channel capacity. his further explains and reinforces equation [12].However, channel capacity gets progressively smaller as the noise increases. Capacity is usually expressed in bits-per-usage (bits per output), or bits-per-second (bits/s). The Shannon-Hartley theorem states that the channel capacity (C) is given by:
Here,
Information Divergence
Information divergence is a measure of dissimilarity of content of two probability distributions. This is a general concept that is used across various domains to compare distributions and the information content of the same. In a lot of machine learning objectives, it can be used as an approximation of the form
There is a large variety of information divergences. Most of them are distance metrics. We are covering one of them in the next section.
Relative entropy or Kullback–Leibler divergence
KL divergence stands for Kullback-Leibler divergence. If we have two distributions
Thus, KL divergence or relative entropy measures the expected number of extra bits required to code samples from
KL divergence gives us a distance between two distributions over the same variable or set of variables. In contrast, variation of information gives us distance between two jointly distributed variables. KL divergence talks about divergence between distributions, while variation of information does the same within a distribution.
KL divergence is not a symmetric measure (i.e.
- Minimizing the forward KL divergence:
- Minimizing the reverse KL divergence:
Both the above optimization functions actually cause different types of approximations. Let us look at each one of them in a little detail:
Forward KL
Let us start with the base equation of Forward KL:
Let us start expanding equation [14]. On substituting the value of KL divergence, with its expansion from equation [12]:
In the above equation, the first element is the cross entropy between P and Q (also denoted by H(p,q) while the second element
The above equation looks similar to the maximum likelihood estimation objective in machine learning exercises. This objective will sample points from p(X) and try to maximize the probability of occurrence of these points under q(X). mean-seeking behaviour, because the approximate distribution Q must cover all the modes (frequent events) and regions of high probability in P.
In short, **"Wherever P has high probability, Q must also have high probability."**Let us look at an example of an approximate distribution for the same:

Figure 13: Approximate distribution for minimization of forward KL divergence
In the above diagram, the approximate distribution Q centers itself between the two modes of P, so that it can have high coverage of both. The 'forward KL divergence' optimization technique does not penalize Q for having high probability mass where P does not.
Application of forward KL divergence
Now, in supervised learning techniques employing 'empirical risk minimization', we use a dataset of samples
-
Regression with Mean-Squared Error Loss: In regression, one of the significant loss functions is the mean-squared error. We aim to reduce the loss in order to get the most accurate predictions. If the distribution of your estimations can be represented as
which is normally distributed. The negative log-likelihood of this normal distribution can be defined as: , where are the results from the regression function and are the actuals. Minimizing the negative log-likelihood of this normal distribution is hence, equivalent to the mean-squared error loss. -
Classification with Cross Entropy Loss: In this case, the approximate distribution (Q) is the result of the classification model. It is represented as a discrete event distribution parameterized by a probability vector (probability of an event belonging to a particular class). In classification you aim to reduce the cross entropy loss(or log loss) of the predicted results against the ground-truth.
The above logic can be applied to any loss function. This way, we can improve the accuracy of the machine learning models. This concept is widely applied to supervised learning techniques.
Reverse KL
Let us start with the base equation of Reverse KL:
The equation for reverse KL can be written as:
It is known as the mode-seeking behaviour because any sample from the approximate distribution Q must lie within a mode of P (since it's required that samples from Q are highly probable to occur under P). Let us look at an approximate distribution to visualize the same.

Figure 14: Approximate distribution for minimization of reverse KL divergence
As we see here, the approximate distribution essentially encompasses the right mode of P. The reverse KL divergence does not penalize Q for not placing probability mass on the other mode of P.
Application of reverse KL divergence
Reverse KL divergence finds its application in reinforcement learning. The maximum-entropy reinforcement learning objective which is used in reinforcement learning models uses this principle extensively.
Differential Entropy
While applying statistics to information theory, we come across a concept of maximum entropy probability distributions. Let us begin with a binomial event of flipping a coin. If a random variable 'X' represents the toss of a fair coin we have,
Loss functions
Loss functions are basically just objective functions that are applied to a lot of machine learning models. The functions take from the concepts of information theory. While a lot of loss functions are designed on the basis of information content or the entropy of datasets, there are a few others that use simple mathematical operations to measure the accuracy and performance of machine learning models. Let us refer to this image below:

Figure 15: Some key loss functions in classification and regression models
Let us talk about a few loss functions in detail.
Cross Entropy Loss and Log Loss
To understand the definition and application of this loss function, let us first understand that it is used in classification problems. This entropy-based loss function is widely used to measure the performance of classification algorithms that give the probability of a record belonging to a particular class as an output. Cross entropy is the more generic form of another loss function, called the logarithmic loss or log loss, when it comes to machine learning algorithms. While log loss is used for binary classification algorithms, cross-entropy serves the same purpose for multiclass classification problems. In other words, log loss is used when there are 2 possible outcomes and cross-entropy is used when there are more than 2 possible outcomes.
These loss functions quantify the price paid for the inaccuracy of predictions in classification problems by penalizing false classifications by taking into account the probability of classification. The generic equation of cross entropy loss looks like the following:
Here, ‘M’ is the number of outcomes or labels that are possible for a given situation and 'N' is the number of samples or instances in the dataset. ‘
Let us assume a problem statement where one has to predict the range of grades a student will score in an exam given his attributes. If there are three possible outcomes: High, Medium and Low represented by [(1,0,0) (0,1,0) (0,0,1)]. Now, for a particular student, the predicted probabilities are (0.2, 0.7, 0.1). This indicates the predicted range of scores will most likely be ‘Medium’ as the probability is the highest there. Hence, the cross-entropy loss would be given as
The equation for cross-entropy loss (equation [22]) can be converted into log loss, by accounting for only two possible outcomes. Thus the formula looks something like this:
We have already spoken about KL divergence as a loss function for both regression and classification problems. Let us look at a few other loss functions.
Focal Loss
Focal loss is an improvement of cross-entropy loss often used for object detection and neural networks. In problems like object detection, a major issue is caused by class imbalance due to the presence of large number of easily-classified background examples. Focal loss is one such loss function that tries to accommodate for this class imbalance.
This loss function is a dynamically scaled log loss function, where the scaling factor

Figure 16: Focal loss adds a scaling factor to standard cross entropy loss
Here, we see that the focal loss function adds a factor
There are several other functions that use probability-based concepts, not necessarily based on entropy and information content. You can explore their use and application according to your requirements and the kind of model you are trying to evaluate.
Learning Rate
Learning rate, also called step-size, is a model-hyperparameter that tells us how to adjust the weights of our model network with respect to the loss gradient function. This concept comes from the optimization functions we saw previously. When applied to machine learning, learning rate helps determine how to change the parameters of a model for it to converge the best, or have the most accuracy. In other words, if we have a hypothesis or model represented in the following manner:

Figure 17: Effect of learning rate on loss function of a model
As we see above ([17]), the learning rate cannot be set either be too high or too low. This is because, with a very high learning rate, the next point in the equation [26] above will perpetually bounce haphazardly across the minima of the curve (refer to
[18] below). With the value of

Figure 18: Effect of learning rate on gradient descent of a model
Information Gain
Information Gain is a key concept of information theory that applies significantly to machine learning. While building a machine learning model on an existing dataset, there are several attributes or fields that contribute to the information content of the dataset and thus the accuracy of the model. The addition or removal of these features can alter the performance of the model.
Information gain is the amount of information or entropy that is gained by knowing the value of the attribute. This is given by calculating the difference of the entropy of the distribution after the attribute is added from the entropy of the distribution before it. It basically measures how much “information” a feature gives us about the class. The largest information gain is a desirable state. Often, information gain is a key concept used in building decision trees. Decision Trees algorithms always try to maximize information gain. Information gain of a dataset can be represented by the following formula:
Information Gain is largely used in decision tree models to define the rules and make the necessary splits at each stage.
Information Bottleneck Method
The Information Bottleneck (IB)
Suppose you have a system with input
The information between these variables can be best represented in the following manner:
Here
Application of IB method in Machine Learning
- Information Bottleneck method can widely be used in dimensionality reduction. This is because we need to compress the base dataset into its most concise form i.e. reduce the dimensions (attributes) in a dataset so as to retain the maximum information contained in the base dataset. We need to strike a balance between the number of attributes in the dataset and the information those attributes carry collectively.
- IB method also finds its application in clustering. Clustering is viewed as lossy data compression because the identity of individual points is replaced by the identity of the cluster to which they are assigned. Information theory is relevant in this context as two points can be clustered together if this merger does not lose too much information about the relevant variable. For instance, you can improve the performance of K-means clustering to converge at the best possible clusters with maximum information using the minimization constraint as defined in equation [27].
- IB method can also be used in another specific case of clustering i.e. topic modelling and document summarization and clustering. For this, it first generates a partitioning of the words (with encoded words:
), which is supposed to preserve information about the documents. Then, the original document representation is replaced by a representation based on the word-clusters. Then, a partitioning of the documents is found that preserves information about the words.
Rate Distortion Theory
In information theory, rate distortion theory describes lossy data compression i.e. the method of compressing data to the minimum number of bits such that it can be reconstructed at the other end of the channel. Rate distortion theory helps determine the minimal number of bits per symbol, as measured by the rate
In the most conventional cases, distortion is measured as the expected value of the square of the difference between input and output signal (i.e., the mean squared error). Let us consider a channel consisting of an encoder and a decoder.

Figure 19: Rate distortion encoder and decoder
Here,
- Hamming Distortion
- Squared-error Distortion
Information Theory in Feature Engineering and Feature Extraction
Knowledge discovery is a process that helps you engineer features or attributes in a base dataset to improve the performance of the machine learning models. Information theory has a lot of 'information measures' or metrics that can help you evaluate the importance and relevance of each new attribute that you develop. For instance, if you develop new attributes in a dataset, you should use measures like mutual information and conditional entropy to evaluate how significant an explanatory variable is with respect to the target or the dependent variable.
We have already seen in the sections above that conditional entropy determines how two variables are correlated. If

Figure 20: Information Measures that can be used as learning and content measures
An automated, relatively new of method of deriving and creating features is feature learning. It helps you automatically discover (or learn) the data transformations and representations needed for feature detection in a dataset. You can conduct two types of feature learning techniques: 1) Supervised: where features are learned using labeled input data, and 2) Unsupervised: where features are learned with unlabeled input data. Rate distortion theory is widely used in feature learning- both supervised and unsupervised. If
Recent Works
In 2006, Hild II et. al. introduced an information theoretic approach to feature extraction in their paper Feature Extraction Using Information-Theoretic Learning
The proposed method called the MRMI-SIG method replaces the entropy terms in the above equation with a specific form of Renyi's quadratic entropy [34]. This leads to the following MRMI-SIG information-theoretic criterion for feature extraction.
The proposed methods extracts features from the raw dataset such that the second term on the right hand side is maximized. This would means that different data points from the same class (in the context of classification) would be very close to each other in the new output features space. To prevent a trivial solution, wherein all features from all classes overlap perfectly, we look at the first term on the right hand side of the equation above. This term denotes the spread measure the of the data irrespective of the class and is maximized in the equation.
In a more specific use case of Fault Diagnosis of Reciprocating Machinery, published by Huaqing Wang et. al.
Information Theory in Feature Selection
While feature engineering includes generation of data, feature selection is a key step in machine learning where you select the most important and relevant features for the given problem statement. Information theory is a key concept used in this step. You can design your optimization function using measures from information theory. Let us look at a few possible techniques.
Mutual Information
As we see in equation [2], Shannon's definition of entropy relies on class prior probabilities. Let us also factor condition entropy in from equation [4]. Let us assume a classification problem with class identities of the target variable represented as 'C'. If 'X' represents your feature space vector, the uncertainty of the class identity can be quantified using the conditional entropy:
The amount by which the class uncertainty is reduced after having observed the feature vector 'X' is called the mutual information,
- Lower Bound: A lower bound to the probability of error when estimating a discrete random variable 'C' from another random variable 'X' can be defined using Fano's bound. It can be represented as:
- Upper Bound: The upper bound that can be set on the probability error can be represented as follows:
Application of optimization of mutual information for feature selection
The idea of using mutual information is to design an objective function that runs on your high dimensional training data. Let us represent the training dataset as

Figure 21: Feature selection by maximizing the mutual information between class labels and transformed features.
Renyi Entropy
We know that mutual information can be computed using probability mass functions. Histograms are one of the most popularly used probability mass functions. However, they are parametric. The issue with parametric methods of estimating information measures is that they work well with 2 or 3 variables. However, with non-parametric methods, you can evaluate and compare multiple variables. This is ideal for high-dimensional data. One of the non-parametric evaluations of entropy in the Renyi Entropy.
Renyi’s quadratic entropy is a generalized form of Shannon's entropy that we have covered earlier. It can be represented in the following manner:
The above metrics can then be used to compute mutual information of a class variable with respect to the features. The aim would be to select features such that the mutual information is maximized.
Recent Works
In 2012, Gulshan Kumar et. al.
Information Theory in Model Selection
Model selection is an important bit in machine learning. With an increasing number of algorithms available for both supervised and unsupervised, it is necessary we choose the best model. This means we also need to penalize model for complexity when the model introduces more complexity than what is needed to fit the regularities of the data. We need to find a model that has an optimal goodness-of-fit and generalization (or generalizability). Generalization basically helps you avoid overfitting of the model. It is claimed that as the model complexity increases, the goodness-of-fit increases but the generalization ability of the model decreases. In other words, a very complex model shows a tendency of overfitting. Below is an image representing the same.

Figure 22: Relationship between generalizability and model fit for varying degrees of model complexity
Let us now look at a few methods of model selection. A few common ways of selecting the best model are as follows:
AIC: Akaike Information Criterion
The Akaike Information Criterion (AIC) is a way of selecting a good model from a set of models. It is based on the concept of KL divergence. In simple terms, it ensures that the best model hence selected minimizes the Kullback-Leibler (KL) divergence between the model and the truth. In general, AIC can be defined in the following manner.
The above equation is slightly modified for small sample sizes (i.e.
While AIC seems to be a reliable measure for selecting models, there are a few caveats in the same. AIC can only compare a given set of models and not determine the absolute quality of a model. In other words, it will give you the best model out of the set of models you have (relative quality), but there might be another model outside your sample set that is a better model. Moreover, it is advised to not use AIC for comparing a large number of models.
BIC: Bayesian information criterion
Bayesian information criterion (BIC) or Schwarz information criterion (also SIC, SBC, SBIC) is yet another information measure for model selection. It is closely related to AIC and can be interpreted in the same manner i.e. the model with the smallest BIC value is the best model. It can be defined as:
One advantage of using BIC over AIC is that AIC generally tries to find an unknown model that has a high dimensionality. This means that all the models might not be true models in AIC. On the other hand, the Bayesian Information Criteria or BIC comes across only true models. This also implies that BIC is more consistent as compared to AIC while estimating for the best model.
MDL: Minimum Description Length
It is a complex concept based on algorithmic coding theory that represents machine learning models and data as compressible codes. The working principle of MDL for model selection is as follows: The best model is the one that provides the shortest description length of the data in bits by “compressing” the data as tightly as possible.. In other words, this means that the model that requires the least number of bits to describe the actual data is the best. Like the other two methods described above, you need to choose a model with the least MDL (minimum description length).
There are multiple methods to estimate the value of an MDL for a model. Some of them are:
- Fisher Information Approximation (FIA)
- Normalized Maximum Likelihood (NML)
The detailed description of these techniques are beyond the scope of the paper currently.
Information Theory in Regression
We have studied how KL divergence can be used in regression to reduce the mean -squared loss error. Let us also cover briefly how mutual information and linear regression might be highly related.
We know from equation [9] that mutual information can be defined as
Now, we know that r-squared
Information Theory in Classification
We have covered the concept of cross entropy loss and log loss as standard loss functions for a lot of classification algorithms. These loss functions are used both in binary classification as well multiclass classifications.
These loss functions can be used to refine the performance of your classification algorithms. You can refer to equation [22] for the generic form of cross entropy loss. A more custom form of the equation for binary classification is the log loss function.
We also saw how entropy is used to build decision trees. Entropy and information gain are used to construct each step of a decision tree. This can help you find the most relevant feature for a particular split in a decision tree. KL divergence is yet another significant information measure used in classification.
Information Theory in Clustering
Clustering is a kind of unsupervised learning problem in machine learning. The goal of (hard) clustering is to assign data instances into one of the groups (clusters) such that the instances in the same cluster exhibit similar properties.We saw in the earlier sections how the Information Bottleneck method can be used for clustering by maximizing compression of individual data points into clusters while ensuring that the loss of information is reduced (or the mutual information is maximized).
Rate-distortion theory is also used in clustering. It finds application in grouping input data into clusters such that the visualization is now driven by these groups instead of the individual elements. If the original data is also represented by
-
hard clustering, where each data element only belongs to one cluster and, thus,
for a specific (correct) cluster and for the other clusters; and -
soft clustering where each data element is assigned to each cluster with a certain probability (in general, different from 0). Then, clustering can be seen as the process of finding class-representatives
(or cluster centroids), such that the average distortion is small and there is a high correlation between the original data and the clusters .
Furthermore, we can use the concept of mutual information for information theoretic clustering.
Mutual Information Criterion for Information Theoretic Clustering
Let us assume that 'Y' represents the cluster identities for your data elements and 'X' defines the features or the variables defining the attributes of these data points. The objective of clustering would be to maximize the mutual information of X and Y i.e.
From equation [9], we know that
Conclusion
The use of information theory extends beyond the applications described in this paper. Information theory can also be used in applications like selection of distance metrics for algorithms like KNN, creation of factor graphs for Bayesian Networks etc.
There are basically two modes of applying information theory in the machine learning:
- Apply fundamental information measures and concepts like entropy, mutual information, KL-divergence as objective functions or regularization terms in an optimization problem. This will help you improve the performance an existing algorithm or model.
- Develop new algorithms and techniques using concepts from sophisticated information theory, such as rate-distortion theory and coding theory. This might help you provide additional insights for existing machine learning techniques and in that process, develop improvised versions of the existing algorithms.
References
- <>. Retrieved from http://colah.github.io/posts/2015-09-Visual-Information/
- Stone, James V;
<>. arXiv:1802.05968v3
- <>. Retrieved from https://dibyaghosh.com/blog/probability/kldivergence.html
- <>. Retrieved from https://www.inference.org.uk/itprnn/book.pdf
- Lin, Tsung-Yi; Goyal, Priya; Girshick, Ross; He, Kaiming; Dollar, Piotr;
<>. arXiv:Physics/0004057v1.
- <>https://heartbeat.fritz.ai/5-regression-loss-functions-all-machine-learners-should-know-4fb140e9d4b0
- <>. Retrieved from https://medium.com/coinmonks/what-is-entropy-and-why-information-gain-is-matter-4e85d46d2f01
- Tishby, Naftali; Pereira, Fernando C.; Bialek, William
<>. arXiv:Physics/0004057v1.
- Rooyen B. V.; Williamson, R;
<>. ArXiv abs/1504.00083 (2015)
- <>. Retrieved from https://www.johndcook.com/blog/2018/11/21/renyi-entropy/
- <>. Retrieved from https://www.r-bloggers.com/how-do-i-interpret-the-aic/
- <>. Retrieved from https://faculty.psy.ohio-state.edu/myung/personal/model selection tutorial.pdf
- Wei, Xiaokai;
<>. 2011
- Kenneth E. Hild, II; Deniz Erdogmus; Kari Torkkola, and Jose C. Principe;
<>. IEEE Trans Pattern Anal Mach Intell. 2006 Sep; 28(9): 1385–1392.
- Wang H, Chen P.
<>Sensors (Basel). 2009;9(4):2415-36. doi: 10.3390/s90402415. Epub 2009 Apr 1. PMID: 22574021; PMCID: PMC3348826.
- Kumar Gulshan, Kumar Krishan
<>Security Comm. Networks 2012; 5:178–185
<>
Recommended for you
High Dimension Data Analysis - A tutorial and review for Dimensionality Reduction Techniques
High Dimension Data Analysis - A tutorial and review for Dimensionality Reduction Techniques
This article explains and provides a comparative study of a few techniques for dimensionality reduction. It dives into the mathematical explanation of several feature selection and feature transformation techniques, while also providing the algorithmic representation and implementation of some other techniques. Lastly, it also provides a very brief review of various other works done in this space.
